Muhammad Sulthan Faraby

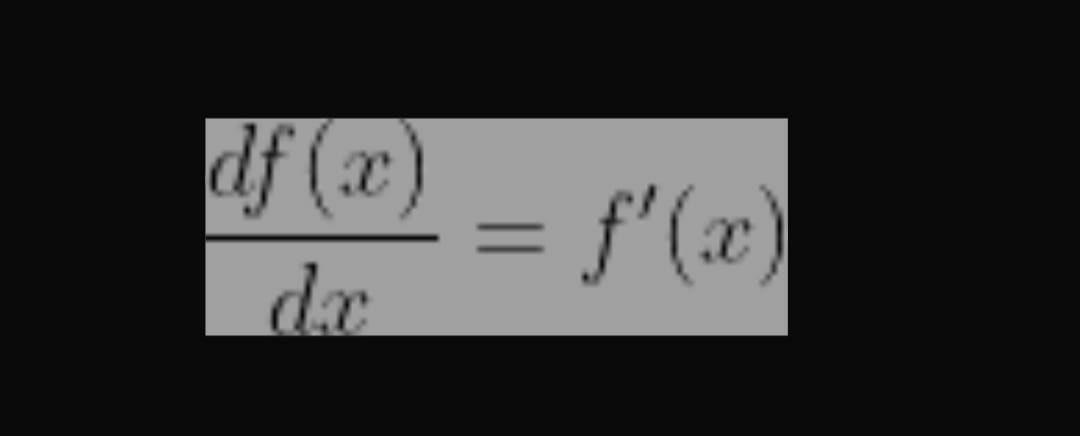
A. Integral taktentu  Integral merupakan anti turunan atau kebalikan dari turunan yang berfungsi untuk menentukan daerah, volume, titik pusat, dan lainnya.  Kalau suatu fungsi f(x) dibalik menjadi f’(x) maka itu merupakan turunan. Nah, jika f’(x) dibalik lagi menjadi f(x), maka itu merupakan integral.  Sebelum ke rumus integral tak tentu, elo perlu paham konsep turunan nih. Gue kasih bayangin dikit tentang turunan secara umum. y= X3 Turunan dari soal ini berapa? dydx = 3×2 Setelah diturunkan seperti ini, lalu dikali silang. dy = 3×2 dx  d(X3) = 3×2 dx Bisa dilihat ya, y diganti dengan X3 Nah, dari sini bisa kita simpulkan ya cara mencari turunan bentuknya akan seperti ini nih. Turunan dari X2 akan menjadi d(X2) = 2x dx Oke, konsep turunan udah ingat lanjut ke materi integral tak tentu lagi. Turunan: Sekarang kita balik, dikalikan silang ya: df(x) = f’(x)dx Kita tambahkan aja lambang integral (∫), menjadi: ∫df(x) = ∫f’(x)dx ∫f’(x)dx = f(x)+C Rumus Integral...

A. turunan fungsi Aljabar dan rumus rumus turunan  Turunan fungsi aljabar adalah fungsi baru hasil penurunan pangkat dari fungsi sebelumnya menurut aturan yang telah ditetapkan. Jika diimplementasikan di dalam grafik fungsi, turunan ini merupakan gradien garis singgung terhadap grafik di titik tertentu. Tingkat turunan fungsi tidak terbatas pada satu tingkat saja, tetapi juga bisa dua tingkat, tiga tingkat, dan seterusnya. Konsep turunan setiap tingkatnya juga sama. Hanya saja, fungsi yang diturunkan berbeda-beda karena mengacu pada hasil turunan sebelumnya. Notasi turunan fungsi aljabar seperti berikut: Seperti yang telah disebutkan di atas, jikaturunan fungsi aljabar merupakan perluasan dari materi limit fungsi sehingga dapat didefinisikan seperti berikut: Rumus Turunan Aljabar Setelah memahami tentang pengertian dari turunan fungsi aljabar, hal yang perlu Sobat Pintar pelajari adalah rumus dari turunan fungsi aljabar. Rumus turunan fungsi aljabar ini terb...

A. limit fungsi Al Jabar Pada dasarnya, limit adalah suatu nilai yang menggunakan pendekatan fungsi ketika hendak mendekati nilai tertentu. Singkatnya, limit ini dianggap sebagai nilai yang menuju suatu batas. Disebut sebagai “batas” karena memang ‘dekat’ tetapi tidak bisa dicapai. Lalu, mengapa limit tersebut harus didekati? Karena suatu fungsi biasanya tidak terdefinisikan pada titik-titik tertentu. Meskipun suatu fungsi itu seringkali tidak terdefinisikan oleh titik-titik tertentu, tetapi masih dapat dicari tahu berapa nilai yang dapat didekati oleh fungsi tersebut, terlebih ketika titik tertentu semakin didekati oleh “limit RUMUS: Dalam ilmu matematika, konsep limit ini ditulis berupa: Maksudnya, apabila x mendekati a tetapi x tidak sama dengan a, maka f(x) akan mendekati L. Pendekatan x ke a ini dapat dilihat dari dua sisi, yakni sisi kiri dan sisi kanan. Nah, dengan kata lain bahwa x juga dapat mendekati dari arah kiri dan arah kanan sehingga nantinya akan menghasilka...